16 Mar 2020
Rings and Double Bond Equivalents
The RDB rule (for Rings and Double Bonds, also sometimes DBE or RDBE for Rings and Double Bond Equivalents) is a versatile tool in mass spectrometry interpretation. It is one of the first tricks one learns when starting to dabble in MS, and it is so widely applicable that it almost seems to have magical properties. The standard definition of the RDB rule, as defined by IUPAC (see Reference 1) is “a conventional measure of the degree of unsaturation of an organic molecule” and is calculated by:
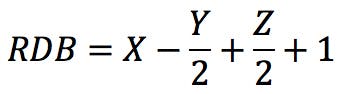
Where X is the number of carbon atoms, Y is the number of hydrogen or halogen atoms, and Z is the number of nitrogen or phosphorus atoms in the molecular formula. An alternative form of the rule could be this:
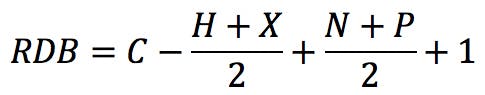
The typical example that we all started with is benzene, C6H6 . The RDB value is:
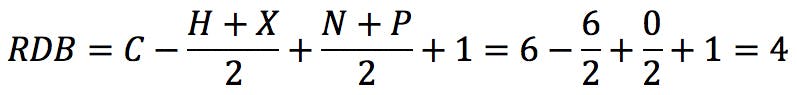
How does one interpret this number? If we draw the Kekulé structure of the molecule,
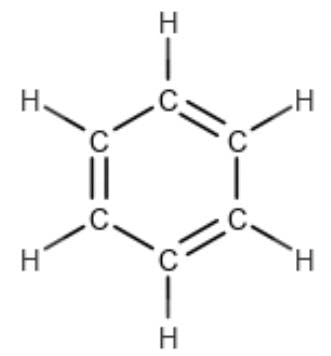
we realise that three degrees of unsaturation are “taken up” by the three double bonds, whilst the fourth is spent in closing the ring itself. The RDB rule was introduced to a generation of mass spectrometrists by McLafferty and Turecek in their book ‘Interpretation of Mass Spectra’ (Reference 2). They did not explain the derivation of the formula, although they attributed the technique to a 1983 paper by Valdo Pellegrin (Reference 4). So how did Dr. Pellegrin arrive at this calculation? Why are some elements added, while others are subtracted? Why are some of them divided by two? And what is that one doing there at the end!?
Saturated and Unsaturated Hydrocarbons
A saturated hydrocarbon is a compound that has only single bonds and therefore cannot undergo addition reactions. An unsaturated molecule is one that has multiple bonds and can undergo addition reactions (Reference 4). Alkanes, the simplest saturated compounds, have the general formula CnH2n+2. Since carbon has four valence electrons, each carbon atom added to the structure introduces two hydrogen atoms, except for terminal carbons which introduce three:
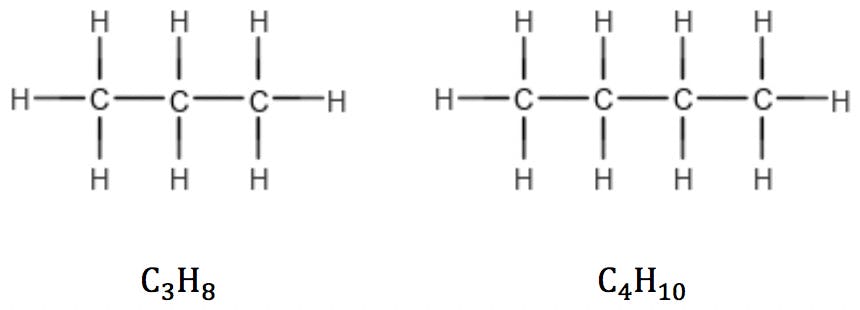
This rule is valid for linear as well as branched alkanes:
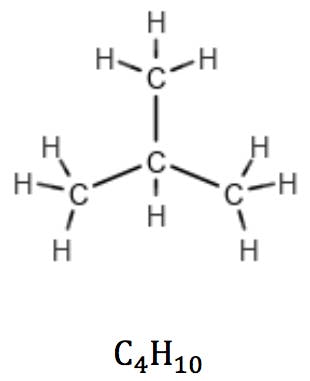
In cycloalkanes, however, the number of hydrogens is reduced by two due to a pair of carbon atoms expending one valence each to “close” the ring. Their general formula therefore is CnH2n:

Alkenes with one double bond (one π bond) also have the general formula CnH2n, revealing the presence of one unsaturation in the structure:
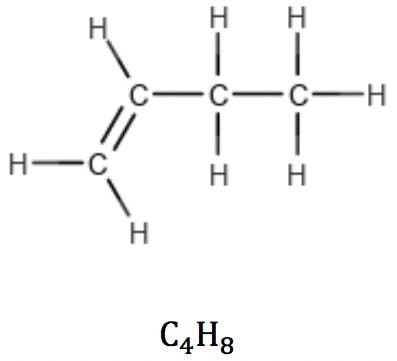
Multiple double bonds and triple bonds (two π bonds) reduce the number of hydrogens accordingly:
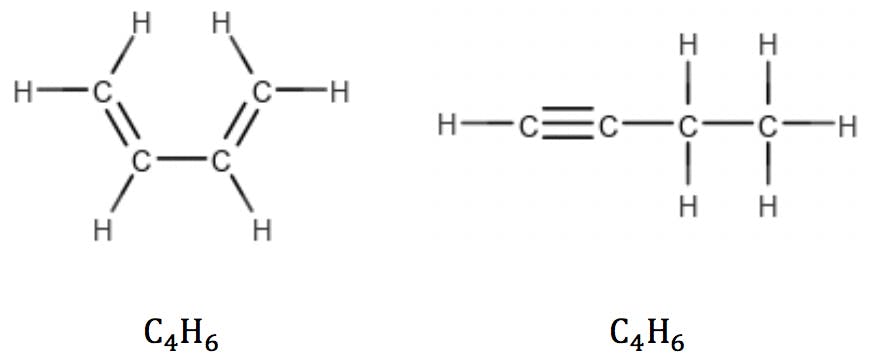
So, the following simple rule could be suggested: for a molecule containing C carbon atoms, the number of hydrogens (H) plus the number of rings and double bonds (RDB) should be equal to 2C+2 in order to saturate all carbon valences.

From this general observation, we can get a first formulation for the RDB rule:
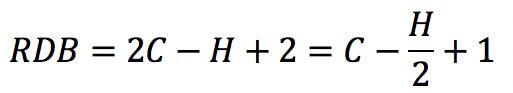
Structures with Heteroatoms
This simple formula accounts for alkanes, alkenes and alkynes, as well as their cyclic counterparts. However, all these compounds contain only carbon and hydrogen. What happens when heteroatoms are introduced into the structure?
Halogens
Halogens are the simplest case. Since they have the same valence as hydrogen, they simply “substitute” H in the structure and also in the formula:
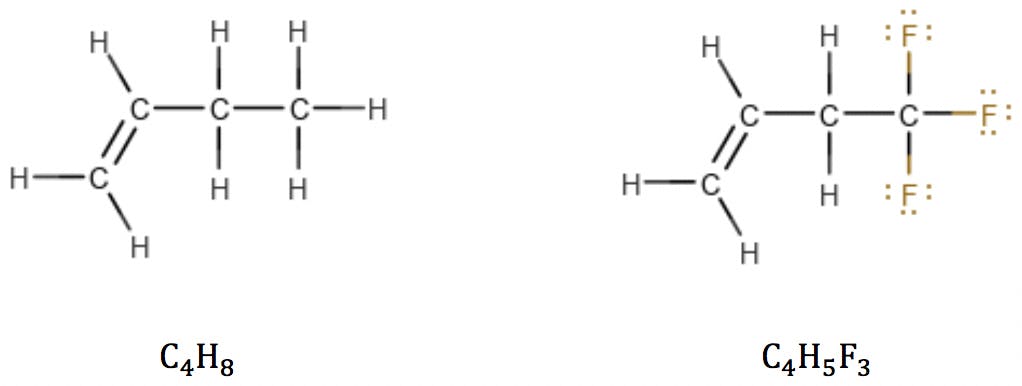
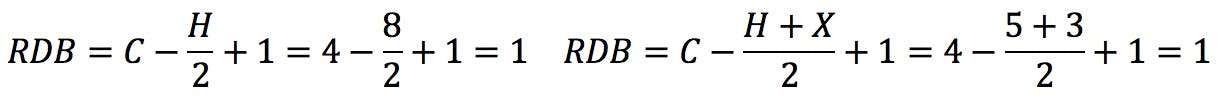
Oxygen
Oxygen atoms are also simple: in alcohols and ethers, oxygen simply “bridges” adjacent atoms, having no effect on RDB:
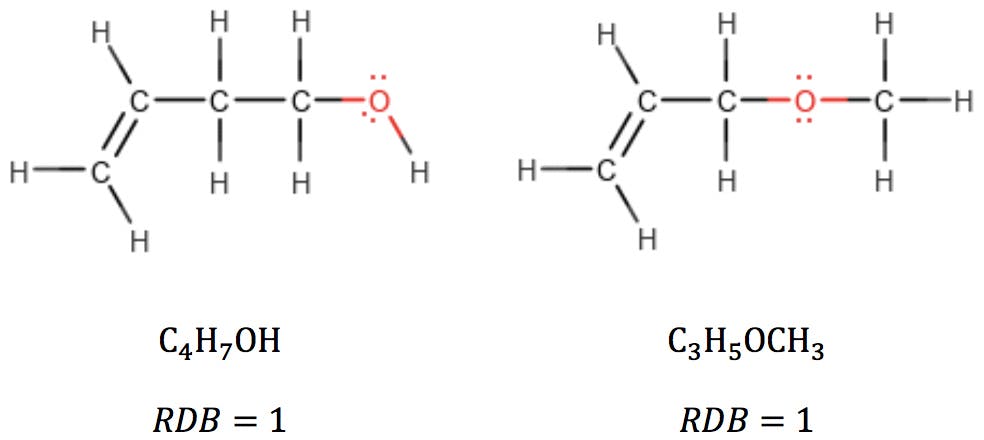
When oxygen is part of a carbonyl group, however, it can be thought of as subtracting two hydrogens from the structure:
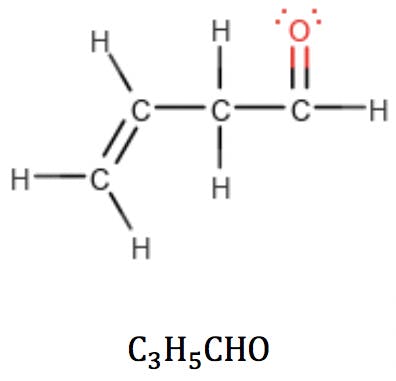

But this “subtraction” is not a problem: the new RDB value correctly reflects the fact that the carbonyl group has introduced a double bond in the structure. This provides a powerful clue as to how to arrange the atoms: it tells the analyst that this oxygen-containing compound is an aldehyde or a ketone, but not an alcohol or an ether.
Nitrogen
Nitrogen, on the other hand, having valence three, introduces some interesting changes:

Adding a nitrogen in a terminal position introduces two hydrogens into the structure, not three as carbon does. Adding a nitrogen in mid-chain adds one hydrogen, instead of two. In both these types of structure, the addition of a nitrogen leaves room for one fewer hydrogens than the addition of a carbon in an equivalent position would.
Each nitrogen atom therefore subtracts one hydrogen from the calculation:
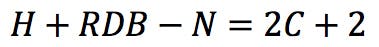
Rearranging this expression, we get the classic RDB formula:
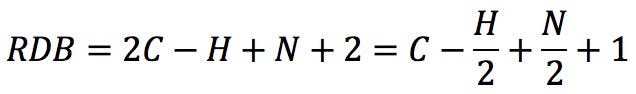
Applying the formula to the amines above:
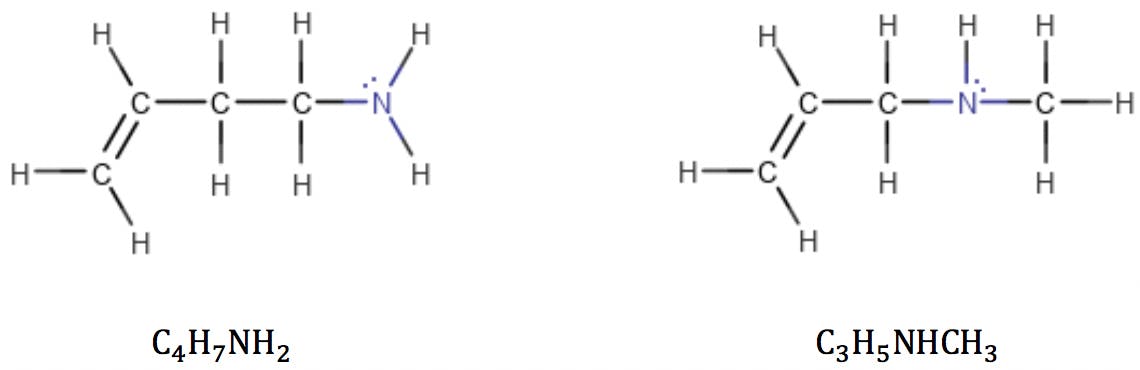
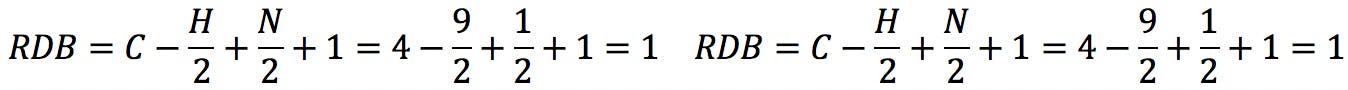
Imines, like ketones and aldehydes, fit this formula as well. The RDB calculation reflects the introduction of a new double bond in the structure:
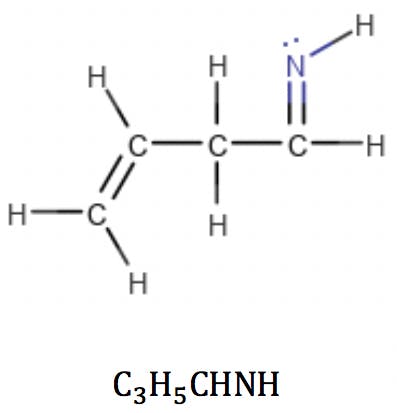
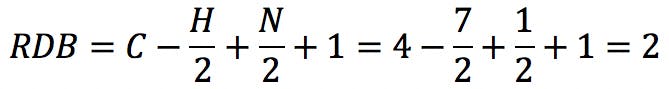
Limitations and New Approaches
Sulphur behaves like oxygen when it reacts with valence two, and phosphorus in the same way as nitrogen when it has valence 3; i.e., sulphur does not appear in the RDB calculation but phosphorus can be added to the formula thus:
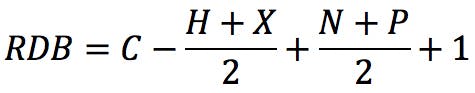
However, we must be mindful that sulphur and phosphorus belong to the third period of the periodic table and can react with higher valence numbers. When sulphur has valence 6, the RDB formula fails:
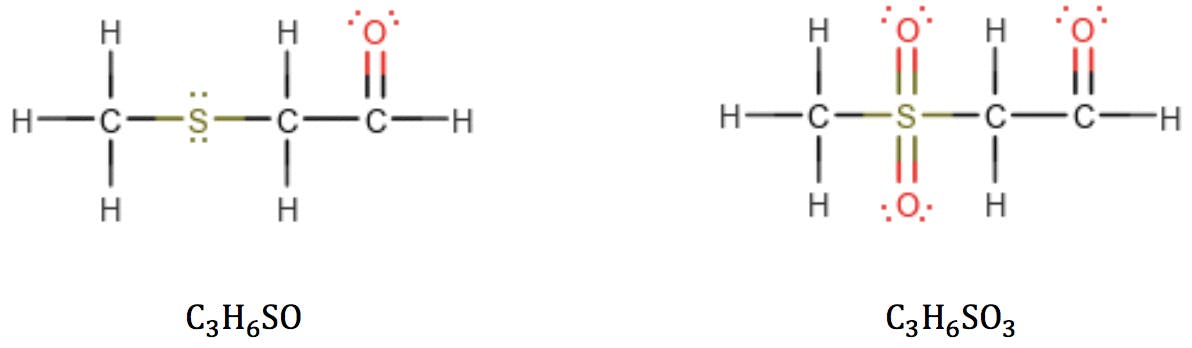
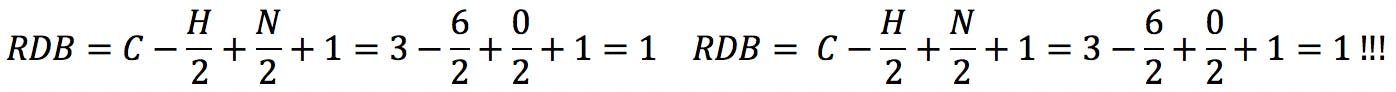
The same problem is encountered with phosphorus in valence state 5:


These problems are caused by the intrinsic assumption that the constituent elements react with their lowest formal valence. This assumption is clearly wrong in some cases, but necessary when one is trying to elucidate the structure of an unknown substance. McLafferty and Turecek acknowledged the fact and cautioned that the rule does not account for double bonds formed by elements with higher valence.
There have been attempts to introduce alternative solutions to this problem, as described for example in Reference 5. Badertscher and his co-workers suggest the following generalised formula to calculate the degree of unsaturation of a compound:
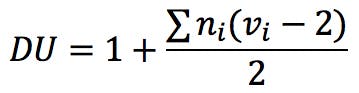
In this equation, vi is the formal valence of an element, and ni is the number of atoms of that element in the molecular formula. Applied to uridine phosphate, for example, we would correctly obtain the number of rings and double bonds:
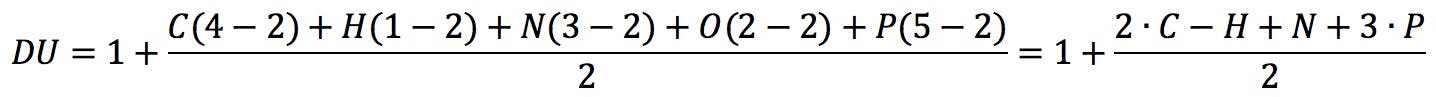
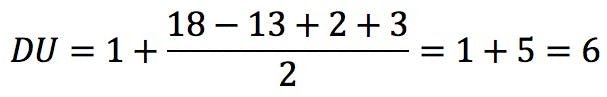
Badertscher et al. further claim that their calculation can be used with charged species – RDB, confusingly, gives half-integer results for even-electron ions and integer results for odd-electron ions – and compounds with non-covalent bonds, such as hydrogen bonds.
Despite its limitations, the RDB rule is of great practical importance thanks to its simplicity and applicability, and we predict it will be taught and utilised for years to come.
References
1. Definitions of Terms Relating to Mass Spectrometry (IUPAC Recommendations 2013); DOI: 10.1351/PAC-REC-06-04-06
2. McLafferty, F. W., Turecek, F. Interpretation of Mass Spectra, 4th edition, University Science Books, 1993
3. Pellegrin, V. Molecular formulas of organic compounds: the nitrogen rule and degree of unsaturation, J. Chem. Educ. 1983, 60, 8, 626
4. McMurry, J., Organic Chemistry, 3rd edition, Brooks/Cole Publishing Co., 1992
5. Badertscher et al., A Novel Formalism to Characterize the Degree of Unsaturation of Organic Molecules, J. Chem. Inf. Comput. Sci. 2001, 41, 4, 889-893